Tensors in Large Language Models

Shapes in Transformers Models

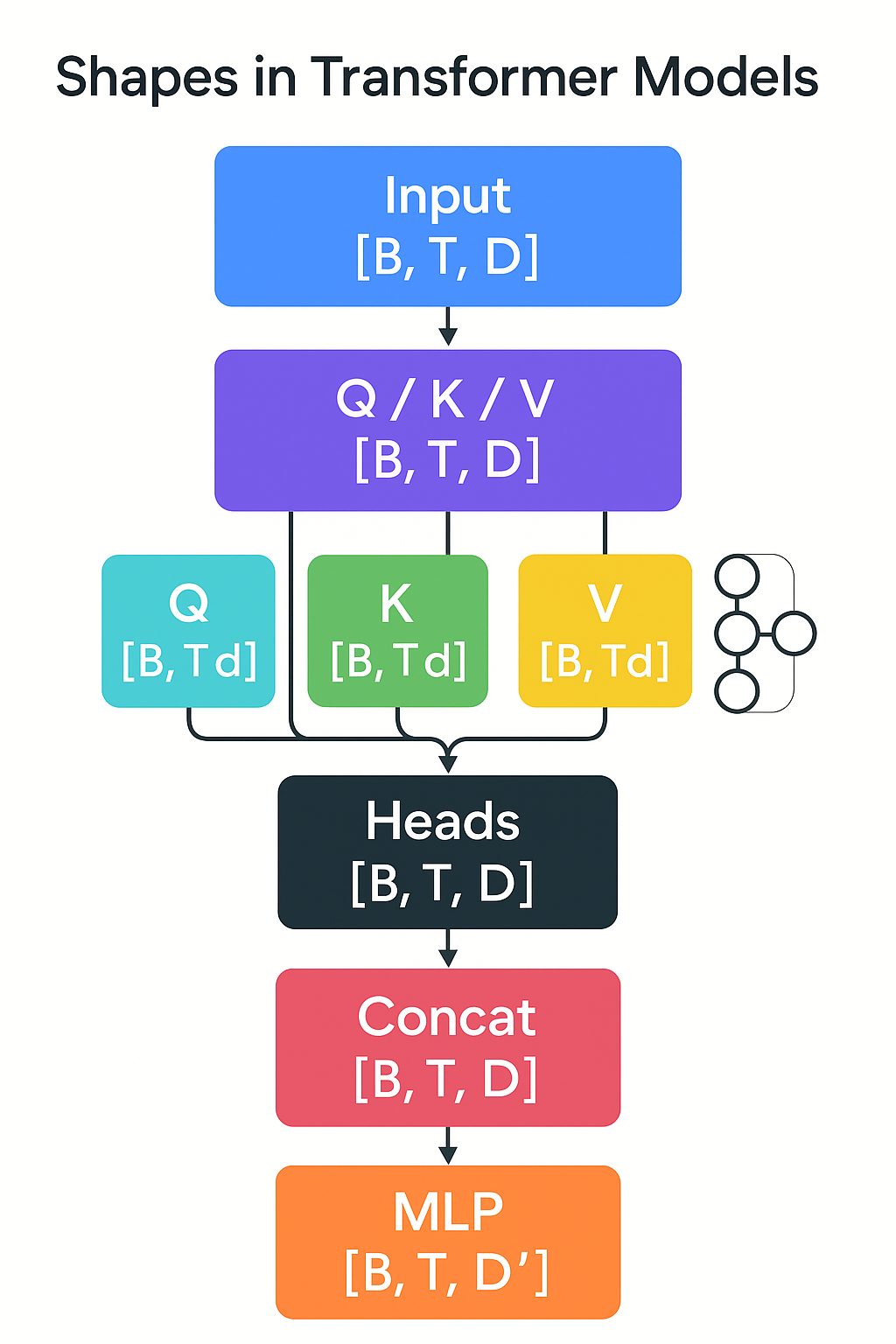
Table of Contents

What is a Tensor?

A tensor is just a multi-dimensional array with: - shape (sizes along each axis), - dtype (numeric type: fp32, bf16, fp8, int8…), - layout/stride (how it’s stored/stepped in memory).

In LLMs, almost every operation is tensor algebra: embedding lookups, batched matmuls, convolutions over time (attention), non-linearities, normalizations.

⸻

⸻

Shapes, Dtypes, Layout

Shape examples: - [B, T, D] = batch, sequence length, hidden width. - [B, nH, T, Dh] = per-head attention (nH heads, head dim Dh). - [V, D] = vocab embedding table.

Dtype trade-offs: - fp32 training is precise but slow/memory-heavy. - bf16/fp16: standard for training. - int8/fp8: inference-oriented, needs calibration. - NF4/FP4: ultra-low precision quant for weights/activations.

Layout: - row-major vs col-major affects BLAS kernels. - contiguous vs strided: non-contiguous hurts kernel efficiency. - packed heads: [B, T, nH, Dh] vs [B, nH, T, Dh] can change memory locality.

⸻

⸻

LLM Canonical Shapes (B, T, D)

  • Input tokens: X_ids: [B, T]
  • Embeddings: E: [V, D] → X: [B, T, D]
  • Self-Attention:
    • project to Q, K, V: each [B, T, nH, Dh] where D = nH * Dh
    • attention weights: [B, nH, T, T]
    • head concat: [B, T, D]
  • MLP/FFN:
    • expand: [B, T, D] → [B, T, 4D] (often), activate, contract back to [B, T, D]

⸻

⸻

⸻

Embeddings & Tokenization Tensors

  • Token embeddings: E_tok: [V, D]
  • Optional sub-tables: special tokens, adapters, soft prompts E_soft: [P, D]
  • Output (LM head): often tied: E_out = E_tok^T → logits [B, T, V]

Memory note: V is large (e.g., 128k). Tying weights saves parameters; logit matmul dominates when V is huge.

⸻

⸻

⸻

Attention Tensors (Q, K, V, Heads)

Given input X: [B, T, D]:

  • Linear projections:
    • Q = X W_Q, K = X W_K, V = X W_V
    • W_*: [D, D] (or [D, nH*Dh])
    • Reshape → [B, T, nH, Dh]
  • Scaled dot-product per head:
    • Scores = (Q ⋅ K^T) / sqrt(Dh) → [B, nH, T, T]
    • Attn = softmax(Scores)
    • Out_head = Attn ⋅ V → [B, nH, T, Dh]
    • Concat heads → [B, T, D], project with W_O: [D, D]

FlashAttention collapses softmax + matmuls with tiling to cut memory traffic from [T, T] intermediates.

⸻

⸻

⸻

Position & Time: Positional/Timestep Tensors

  • Absolute: learned table P: [T_max, D] added to embeddings.
  • Sinusoidal: analytic [T, D] functions.
  • RoPE: complex rotation of Q/K in head-dim space; no extra params, but needs consistent rotation shapes: apply on [B, T, nH, Dh].
  • ALiBi: bias over distance, avoids explicit position vectors.

All are tensors aligned on the T axis and broadcast over B and nH.

⸻

⸻

⸻

KV Cache: Memory vs Throughput

For autoregressive inference, we store past K, V: - Cache shape per layer: [B, nH, T_total, Dh] for both K and V. - Memory cost (rough): 2 * L * B * nH * T_total * Dh * dtype_size. - Trade-offs: - Larger T_total → faster per-token (reuse past) but high RAM/VRAM. - Quantized KV (int8/fp8) cuts memory; must keep accuracy. - Paged KV/block-KV organizes cache as fixed blocks to reduce fragmentation

⸻

⸻

⸻

Feedforward/MLP Tensors

Typical gated GLU/SiLU FFN: - Expand: W1: [D, D_ff], W3: [D, D_ff], then silu(X W1) ⊙ (X W3) - Project back: W2: [D_ff, D] - Shapes: - Activations: [B, T, D_ff] (often D_ff ≈ 4D) - Params: D*D_ff dominates per layer.

⸻

⸻

⸻

Training-Time Tensors (Grads, Optimizer States)

  • Gradients: same shape as weights.
  • Adam/AdamW states: m, v → 2× the parameter memory.
  • Mixed precision: master fp32 weights + bf16 activations.
  • Activation checkpointing reduces saved activations (recompute in backward).

Rule of thumb: training memory ≈ params (fp16/bf16) + optimizer (≈2× params fp32) + activations (batch-/sequence-dependent).

⸻

⸻

⸻

Tensor Parallelism & Sharding

  • Data parallel: replicate weights, split batches [B].
  • Tensor/model parallel: shard weight matrices along D or D_ff (Megatron-LM style).
  • Pipeline parallel: split layers; micro-batches stream through.
  • Sequence parallel: split T across devices (useful with long context).
  • ZeRO: shard optimizer states/gradients/params across ranks.

Each choice changes the effective tensor shapes per device and the required all-reduce/all-gather patterns.

⸻

⸻

⸻

Quantization, Low-Rank & MoE

  • Quantization:
    • Weights/activations to int8/fp8/FP4/NF4.
    • Tensor-wise vs group-wise scaling tensors (per-channel scales [D] or [groups, …]).
  • Low-Rank (LoRA/QLoRA):
    • Replace W ∈ ℝ^{D_out×D_in} with W + A B where A: [D_out, r], B: [r, D_in], r ≪ D.
  • MoE:
    • Gating tensor G: [B, T, nExperts] (often top-k).
    • Expert FFNs see routed tokens: shapes become ragged; implement with packed blocks for kernel efficiency.
    • Load-balancing loss acts on gating tensor statistics.

⸻

⸻

Tensor Core Math: Throughput Reality

  • GPUs/TPUs peak on dense GEMMs with specific tile sizes.
  • Best throughput when shapes are multiples of hardware tiles (e.g., 64/128).
  • Fused kernels (RMSNorm → QKV → bias → RoPE) minimize reads/writes.
  • Performance killers: non-contiguous tensors, tiny batch/head dims, excessive transposes.

⸻

⸻

Debugging by Shape: Common Pitfalls

  • Q/K/V reshape/order mismatch: [B, T, nH, Dh] vs [B, nH, T, Dh].
  • RoPE applied on wrong dims or after projection merge.
  • KV cache dtype/shape drift across tokens (e.g., bf16 vs fp16).
  • Logits with tied weights: ensure E_tok and LM_head share transposed shape.
  • MoE routing: padding vs packing; silent throughput collapse if not packed.

⸻

⸻

Mini Cheatsheet

  • Embeddings: E[V, D], inputs → [B, T, D]
  • Attention heads: nH = D / Dh, Q/K/V [B, T, nH, Dh]
  • Scores/attn: [B, nH, T, T] (fused via FlashAttention)
  • FFN: D_ff ≈ 4D, shapes [B, T, D_ff]
  • KV cache / layer: 2 × [B, nH, T_total, Dh]
  • Adam states: 2 × params
  • LoRA rank r: extra params r(D_in + D_out)
  • MoE gating: G[B, T, nExperts], top-k Routing

⸻

⸻

Optional images to add

  • A one-panel diagram of shapes through a transformer block.
  • A KV cache memory budget bar chart (bf16 vs int8).
  • A MoE routing sketch (gate → pack → expert FFNs → merge).